L Systems - creating trees

Martin McBride

2019-07-12

In this post we will look further into L Systems and see how they can be used to tree and fern like structures using generativepy. We will make use of the simple turtle system developed in a previous post.

Extending our L System grammar

We will start by creating a simple binary tree like this:

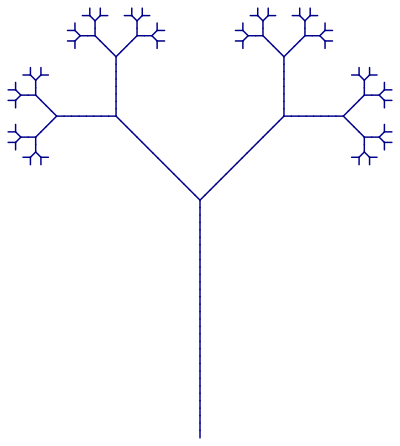
This pattern is the 6th generation of a pattern that starts out as a simple Y shape. Unlike simpler L Systems, it exhibits branching. There are 64 "leaves" in the images. Starting from the first generation (a Y shape) which has 2 leaves, the number of leaves doubles on each generation (2 to the power 6 is 64).

To implement branching, we need to add two extra characters to our L System grammar:

[ doesn't draw anything, but it saves the current turtle position and heading
] also doesn't draw anything, but restores the previous turtle position and heading.

So the string [ABC]XYZ saves the initial position then draws ABC (whatever that might be). It then restores the previous position, and draws XYZ starting from the original position and heading. Notice that ABC and XYZ just represent whatever real operations you might want to perform.

The save and restore operations use a stack, so you can save multiple positions, and they will be restored in the reverse order.

Binary tree parameters

Here are the rules for the binary tree:

F becomes G[+F]-F
G becomes GG
+ becomes +
- becomes -
[ becomes [
] becomes ]

F and G both draw a line length 10. + and - turn left or right by 45 degrees (pi/4).

It is worth looking at the first pass. The initial string F becomes G[+F]-F. Here is what this draws:

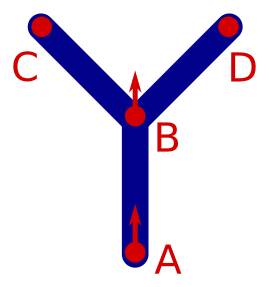
Imagine we start of at point A, with the turtle heading upwards.

G moves 10 units upwards to point B
[ saves the current position (B) and heading (upwards)
+F turns the turtle 45 degrees left and draws 10 units to point C
] restores the previous position. The turtle is placed back at point B, heading upwards, without drawing anything
-F turns the turtle 45 degrees right and draws 10 units to point D

The code

Here is the binary tree Python code:

from generativepy import drawing
from generativepy.drawing import makeSvg
from generativepy.color import Color
from turtle import Turtle
import math

AXIOM = 'F'
RULES = { 'F' : 'G[+F]-F',
          'G' : 'GG',
          '[' : '[',
          ']' : ']',
          '+' : '+',
          '-' : '-' }
ITERATIONS = 6
ANGLE = math.pi/4
LENGTH = 10
SIZE=800


def lsystem(start, rules):
    out = ''
    for c in start:
        s = rules[c]
        out += s

    return out

def draw(canvas):
    s = AXIOM
    for i in range(ITERATIONS):
        s = lsystem(s, RULES)

    turtle = Turtle(canvas)
    canvas.stroke(Color('darkblue'))
    canvas.strokeWeight(2)
    turtle.moveTo(SIZE/2, SIZE-10)
    turtle.left(math.pi/2)
    for c in s:
        if c=='F':
            turtle.forward(LENGTH)
        if c=='G':
            turtle.forward(LENGTH)
        elif c=='[':
            turtle.push()
        elif c==']':
            turtle.pop()
        elif c=='+':
            turtle.left(ANGLE)
        elif c=='-':
            turtle.right(ANGLE)


makeSvg("lsystem-binary-tree.svg", draw, pixelSize=(SIZE, SIZE))

The main things to note here are:

The turtle is moved to position (SIZE/2, SIZE-10), the centre-bottom of the canvas, and turned to point upwards, just after the turtle is created.
We have added the [ and ] cases using the existing Turtle methods push and pop.

Here is the result:

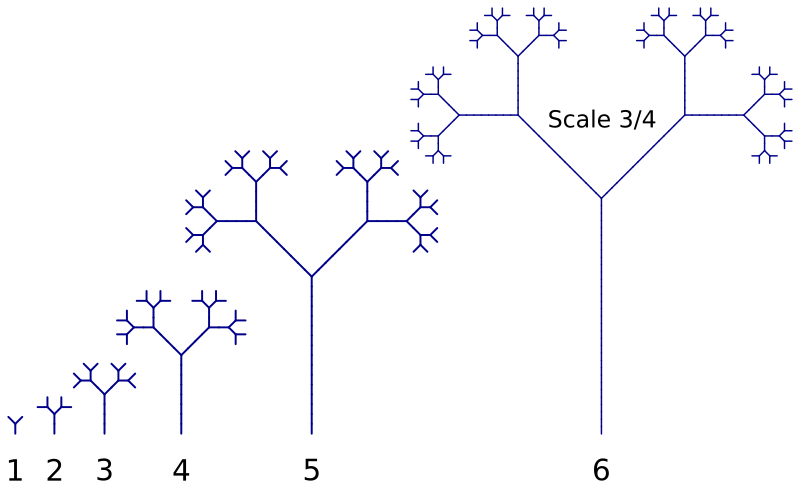
The trees are all at the same scale, except the sixth iteration, which is scaled down very slightly (to 75% of its original size) to fit.

A more realistic plant

We will modify the previous code slightly to create a more realistic looking L System plant.

The first rule is chnaged to:

F becomes G+[[F]-F]-G[-GF]+F

and the angle is changed to 20 degrees. This gives the following basic shape (ie the shape after 1 iteration):

You can follwo this through, step by step, like we did for the binary tree, if you wish. The shape creates after 6 iterations is:

The final code is below. All that has really changed are the rules and angle, a bit of adjustment of the size and position, and all importantly making the plant green instead of blue.

from generativepy import drawing
from generativepy.drawing import makeSvg
from generativepy.color import Color
from turtle import Turtle
import math

AXIOM = 'F'
RULES = { 'F' : 'G+[[F]-F]-G[-GF]+F',
          'G' : 'GG',
          '[' : '[',
          ']' : ']',
          '+' : '+',
          '-' : '-' }
ITERATIONS = 6
ANGLE = 20*math.pi/180
LENGTH = 5
SIZE=800


def lsystem(start, rules):
    out = ''
    for c in start:
        s = rules[c]
        out += s

    return out

def draw(canvas):
    s = AXIOM
    for i in range(ITERATIONS):
        s = lsystem(s, RULES)

    turtle = Turtle(canvas)
    canvas.stroke(Color('darkgreen'))
    canvas.strokeWeight(2)
    turtle.moveTo(SIZE/4, SIZE-10)
    turtle.left(75*math.pi/180)
    for c in s:
        if c=='F':
            turtle.forward(LENGTH)
        if c=='G':
            turtle.forward(LENGTH)
        elif c=='[':
            turtle.push()
        elif c==']':
            turtle.pop()
        elif c=='+':
            turtle.left(ANGLE)
        elif c=='-':
            turtle.right(ANGLE)


makeSvg("lsystem-tree.svg", draw, pixelSize=(SIZE, SIZE))

L Systems - creating trees

Extending our L System grammar

Binary tree parameters

The code

A more realistic plant

Popular tags