A simple turtle in generativepy

Martin McBride

2019-06-28

In this post we will create a simple turtle graphics in generativepy, and use it to recursively plot a Koch curve.

Turtle graphics

You will probably be familiar with turtle graphics. The idea is that you have a graphics cursor that can draw lines as it moves around.

The cursor has an (x, y) position, and also a direction it is pointing in (the heading). The you can tell the turtle to move forward by a certain distance, or to turn through a certain angle to the left or right. By issuing a series of instructions, you can draw various shapes.

To allow for recursive drawing (to create fractal images) turtle graphics can push the current state onto a stack. At some later stage it can pop its previous state (position and heading) and continue from there.

generativepy implementation

Here is the Python code to implement a simple turtle:

import math

class Turtle():

    def __init__(self, canvas):
        self.canvas = canvas
        self.heading = 0
        self.x = 0
        self.y = 0
        self.stack = []

    def push(self):
        state = self.heading, self.x, self.y
        self.stack.append(state)

    def pop(self):
        state = self.stack.pop()
        self.heading, self.x, self.y = state

    def forward(self, distance):
        p1 = self.x, self.y
        self.x += distance*math.cos(self.heading)
        self.y += distance*math.sin(self.heading)
        self.canvas.line(*p1, self.x, self.y)

    def move(self, distance):
        self.x += distance*math.cos(self.heading)
        self.y += distance*math.sin(self.heading)

    def moveTo(self, x, y):
        self.x = x
        self.y = y

    def left(self, angle):
        self.heading -= angle

    def right(self, angle):
        self.heading += angle

This class uses self.x and self.y to store the position, and self.heading to store the current direction. It draws on a generativepy drawing.Canvas object.

push and pop save and restore the current state (x, y and heading) as a tuple, using a list as a stack.
forward moves forward a certain distance, drawing a line on the canvas.
move is similar to forward but moves without leaving a line.
moveTo moves straight to a new (x, y) position without drawing anything.
left and right move the turtle direction through angle, to the k=left or right.

The turtle will draw lines using the stroke colour and weight that is defined when the turtle functions are called.

Drawing a simple figure

Here is some code that draws a simple figure using the turtle (assuming we have a suitable canvas object):

turtle.forward(10)
turtle.left(math.pi/2)
turtle.forward(10)
turtle.right(math.pi/2)
turtle.forward(10)
turtle.right(math.pi/2)
turtle.forward(10)
turtle.left(math.pi/2)
turtle.forward(10)

This sequence (foward, left, forward, right, forward, right, forward, left, forward ) will draw a shape something like this:

Making the figure recursive

We can draw this figure recursively using the following code:

def plot(turtle, level):
    if level < 1:
        turtle.forward(10)
    else:
        plot(turtle, level-1)
        turtle.left(math.pi/2)
        plot(turtle, level-1)
        turtle.right(math.pi/2)
        plot(turtle, level-1)
        turtle.right(math.pi/2)
        plot(turtle, level-1)
        turtle.left(math.pi/2)
        plot(turtle, level-1)

Calling the function with level set to 0

If we call this function with level set to 0, the if statement will be true and the function will just call turtle.forward, which just draws a single line.

Calling the function with level set to 1

If we call the function with level set to 1, the second part of the if statement will execute. This executes the following steps:

calls plot recursively with level set to 0 - draws a single line
turn left
calls plot recursively with level set to 0 - draws a single line
turn right
etc

These steps are identical to the original code. This will draw the same figure as before:

Calling the function with level set to 2

If we call the function with level set to 2, things get more interesting. The second part of the if statement will execute. This executes the following steps:

calls plot recursively with level set to 1 - draws the original figure
turn left
calls plot recursively with level set to 1 - draws the original figure rotated to the left
turn right
calls plot recursively with level set to 1 - draws the original figure back at the original orientation
turn right
calls plot recursively with level set to 1 - draws the original figure rotated to the right
turn left
calls plot recursively with level set to 1 - draws the original figure back at the original orientation

The result is shown below, with the original figure shown in a different colour for each iteration:

The full code

Here is the full code that you can run for yourself. You will also need the turtle code from earlier in this post, which you should save in a file called turtle.py in the same folder.

from generativepy import drawing
from generativepy.drawing import makeImage
from generativepy.color import Color
from turtle import Turtle
import math

def plot(turtle, level):
    if level < 1:
        turtle.forward(10)
    else:
        plot(turtle, level-1)
        turtle.left(math.pi/2)
        plot(turtle, level-1)
        turtle.right(math.pi/2)
        plot(turtle, level-1)
        turtle.right(math.pi/2)
        plot(turtle, level-1)
        turtle.left(math.pi/2)
        plot(turtle, level-1)

def draw(canvas):
    canvas.stroke(Color('darkblue'))
    canvas.strokeWeight(1)
    turtle = Turtle(canvas)
    turtle.moveTo(10, 290)
    plot(turtle, 3)        #Sets the initial level


makeImage("turtle-koch-curve.png", draw, pixelSize=(800, 300), background=Color(1))

You should be able to run this yourself if you have generativepy installed. Here is the output you will get:

Iteration level 1

Iteration level 2

Iteration level 3

Iteration level 4

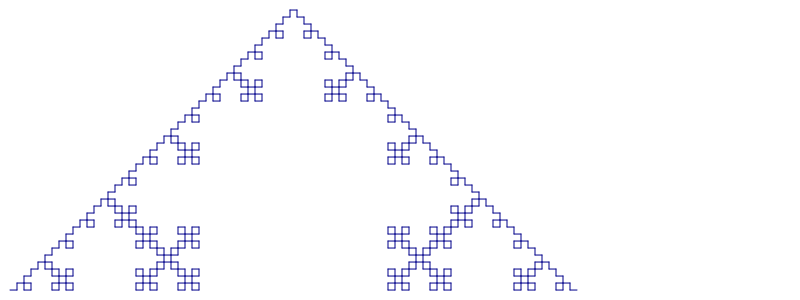
Note that when the level is set to 4, the image is too big to fit the image size we are using. You can either increase the image size, or make the image smaller, or even try a combination of both.

In this case we have made the image smaller by setting the forward distance to to 4 rather than 10 (the turtle.forward(10) line in the plot function).

Conclusion

We have defined a simple turtle system, and used it to draw a Koch curve in generativepy. You can use this to try drawing other fractals such as the Sierpinski triangle. See the article on L Systems for a way make this easier.