Wave shapes

Martin McBride

2021-08-29

If you play the same note on different instruments, it will sound very different. A piano, an oboe, and an electric guitar can all play middle C, but they won't sound the same at all.

The specific sound of a particular type of instrument is called its timbre. One of the major factors that determine the timbre is the shape of the wave. In this article, we will look at various wave shapes that can be used in sound synthesis.

Sine waves

The simplest oscillating system is probably a pendulum - a weight, hanging on a string, swinging backwards and forwards. It turns out that the motion of a pendulum can be modelled by a sine wave.

Other oscillating systems, such as a vibrating string guitar string, can also be modelled by a sine wave. The model isn't perfect. A mathematical sine wave will oscillate forever, but a pendulum or vibrating string will eventually stop due to friction and air resistance.

Here is a 400Hz sine wave, as we saw in the previous article about frequency:

Harmonics

When a real instrument plays a note, it doesn't usually produce a pure sine wave of the note frequency. Most instruments produce additional oscillations at multiples of the main frequency. These are called harmonics:

The fundamental frequency is the true frequency of the note. This is sometimes called the first harmonic.
The second harmonic has a frequency that is twice the fundamental frequency.
The third harmonic has a frequency that is three times the fundamental frequency.
And so on.

We don't hear these harmonics as separate sounds. We hear the effect of all the harmonics added together. What we hear is the fundamental frequency, but with a different wave shape, which makes it sound different.

Here is an example, a simple synthesised instrument that has just three harmonics. The first harmonic is at 400 Hz, and in this example will have an amplitude of 0.7:

The second harmonic is at twice the frequency (so 800 Hz), and we will give it an amplitude of 0.2:

The third harmonic is at three times the frequency (so 1200 Hz), and we will give it an amplitude of 0.4:

All three oscillations happen together at the same time, so the resulting wave is the sum of all three harmonics. Here is the result:

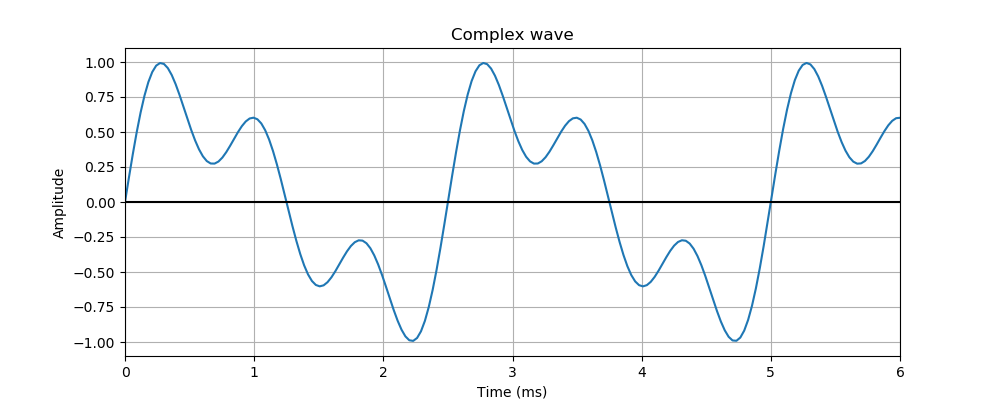
Because the harmonics are all multiples of the basic frequency and are all in step, the result is a wave that has a 400 Hz frequency, but a different shape.

Analysing the frequency components of real instruments allows us to recreate similar sounds, particularly in software synths where we can easily calculate waveforms mathematically. It won't guarantee that the synth will sound exactly like a trumpet or glockenspiel, but it is a step along the way. The same technique can be used to create novel instruments that don't exist in the physical world.

Synthetic waveforms

Electronic and computer synthesisers can create waveforms that can't be easily created by traditional instruments. In particular, square and sawtooth waves are quintessentially electronic sounds. They can sound a bit raw on their own, but they can be further processed to create interesting timbres.

Square wave

A square wave signal only has two values - on or off. The signal switches from one to the other like this:

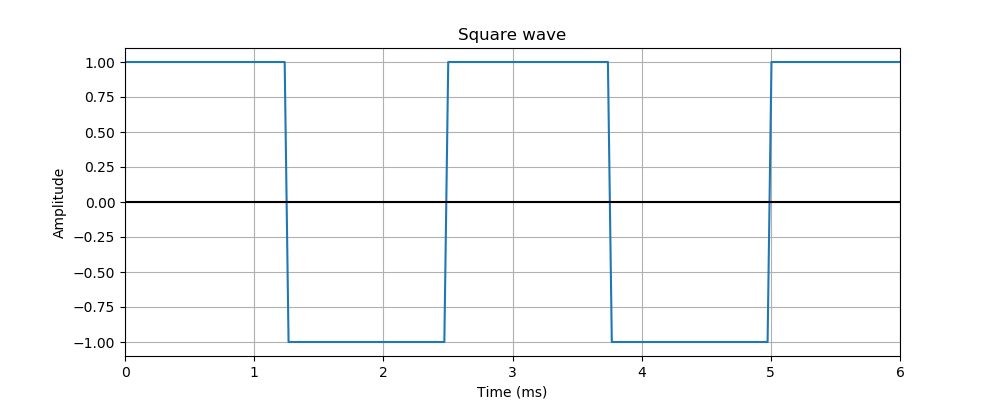
A square wave is a bit like a sine wave, but instead of changing gradually between +1 and -1, it switches quickly between those states.

The main advantage of square waves is that they are very easy to generate. There are some very simple electronic circuits that generate square waves, for example:

A Schmitt trigger can be used to make a square wave oscillator, with just the addition of a resistor and capacitor. The 7414 chip contains 6 Schmitt triggers, so it can be used to create 6 oscillators. It is very low cost and can be used to create polyphonic synths (that is, synths that can play more than one note at a time) very cheaply.
A 555 timer chip is also a good way to create square waves and has the advantage that the frequency can be changed by a control voltage.

Computers can also create square waves very easily. Generating a square wave doesn't require any complex calculations, the CPU just needs to turn an output pin on and off at certain times. This means that even a very cheap CPU can generate sound. Another advantage is that, because the signal generated by the CPU is just a single output pin turning on and off, it can be fed straight to a simple amplifier and speaker. There is no need for a digital to analogue converter (DAC) to convert the digital value to a voltage.

Square waves sound fairly terrible on their own, it is a very harsh signal. They can be used sparingly for effect, but listening to music composed entirely of square waves would be hard on the ears. But square waves have lots of harmonic content, so they can be filtered to make interesting sounds.

A square wave is actually louder than a sine wave of the same amplitude. This is because a signal that jumps rapidly from one value to another carries more energy than a signal that moves smoothly between those values. We will see a more mathematical explanation of this in a later article of Fourier analysis.

Pulse waves

A pulse wave is a more general version of the square wave, where the on and off times are not necessarily equal, like this example:

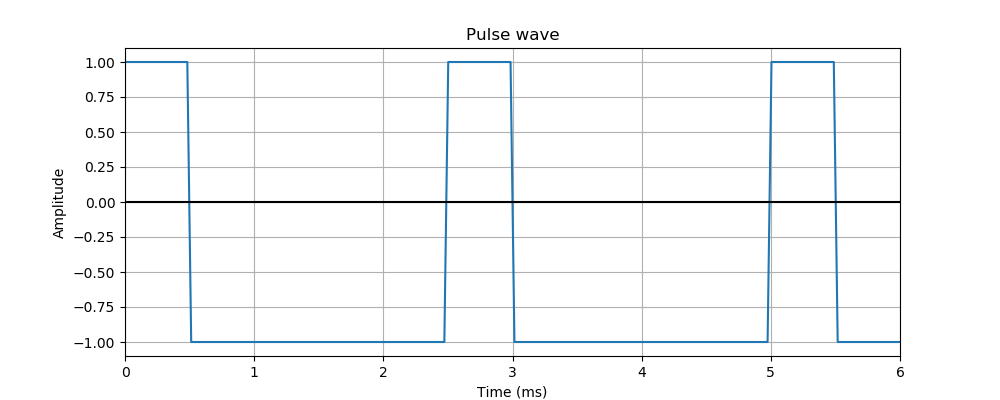
In this case, the sound is on for 20% of the time, off for 80% of the time.

We say that it has a duty cycle of 0.2. A duty cycle of 0.5 corresponds to a square wave

The mark-space ratio is a related measure. It is the on-time divided by the off-time. For a square wave, the mark space ratio is 1:1 (the on and off times are equal). For the pulse above, the ratio is 1:4, ie 0.25, because the off time is 4 times longer than the on-time.

All pulse waves have a similar raw sound, but the duty cycle affects the sound.

Triangle waves

A triangle wave is similar to a sine wave, but the value varies changes as a linear function between the minimum and maximum values

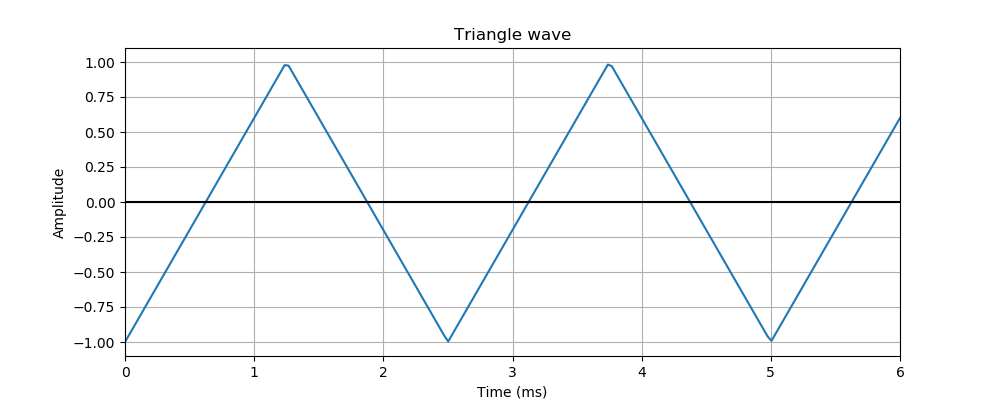
This wave is a little like a sine wave, in that it varies smoothly between the minimum and maximum values. The difference is that it makes an abrupt change in direction at the endpoints (whereas a sine wave changes direction smoothly at the minimum and maximum points).

The sound of a triangle wave is somewhere between a sine wave and a square wave. It still has a harsh and unnatural edge to it, but it is smoother than a square wave.

Triangles can have different rise and fall times:

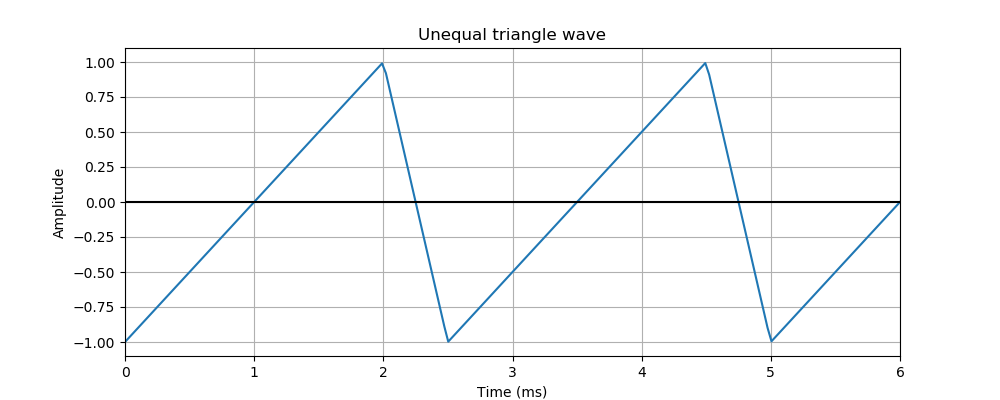
In this case, the wave spends 80% of the time rising, and 20% falling. We would say this has a rise fall ratio of 4:1 because the rising phase is 4 times longer than the falling phase. The rise-fall ratio is analogous to the mark space ratio of a pulse wave.

Sawtooth

A saw wave is a variant of the triangle wave, but it spends 100% of the time rising from minimum to maximum, then instantly jumps back down to the minimum.

It can be thought of as an extreme variant of the triangle wave where the rise fall ratio is 1:0.